What Is a Quaternion in Star Trackers

Quaternions serve as a mathematical tool. They represent rotations and offer a robust, efficient way to calculate and maintain precise orientation.

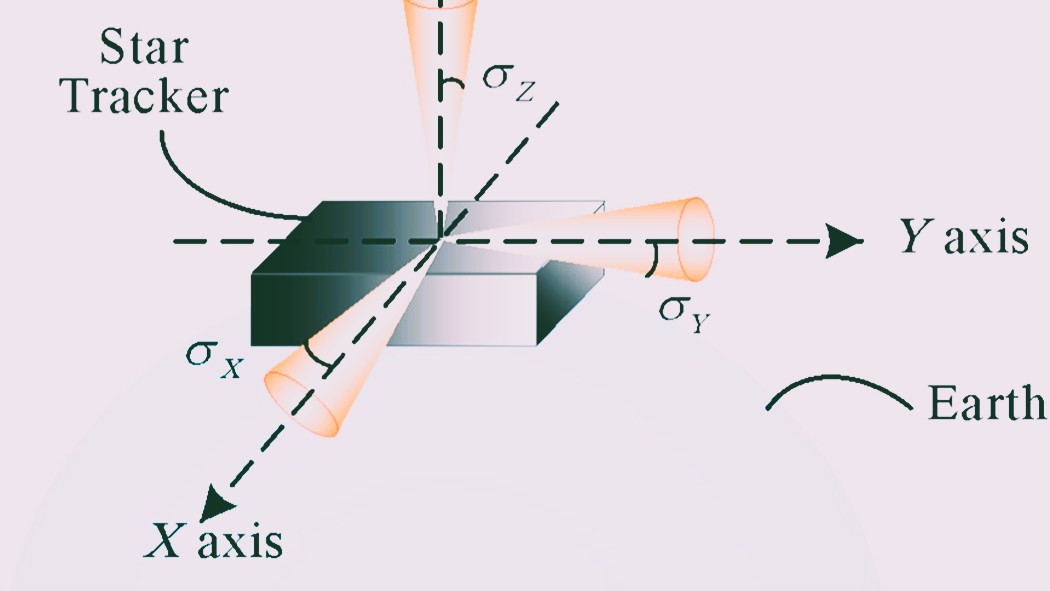
Star trackers rely on the fixed positions of stars in the night sky. They capture star images, compare them with a pre-loaded star catalog, and thus determine the spacecraft’s attitude accurately.

Modern star trackers output data in various formats. Quaternions, as four-dimensional numbers, describe rotations effectively. Moreover, they avoid gimbal lock issues that plague methods like Euler angles, where certain attitudes lose a degree of freedom.

How Star Trackers Generate Quaternion Output

Image Acquisition: The star tracker’s camera captures sky snapshots. It typically uses CCD or CMOS trackers with a wide field of view.

Star Identification: Advanced algorithms match observed bright spots with a database containing thousands of stars. Lost-in-space mode works even when initial attitude is unknown, while tracking mode continuously optimizes estimates.

Vector Calculation: For each matched star, the system computes unit vectors in both the tracker coordinate frame and the inertial frame.

Attitude Estimation: Using methods like QUEST, the system calculates the quaternion. This quaternion best transforms body vectors to inertial vectors.

Output and Integration: The quaternion outputs at high frequency. It feeds into the spacecraft’s attitude control system, which then makes real-time adjustments via reaction wheels or thrusters.

Advantages of Quaternions in Star Trackers

Why do engineers choose quaternions over other representations? The advantages stand out clearly:

Efficiency: Quaternions require only four parameters. Therefore, they save computational resources on power-limited spacecraft.

No Gimbal Lock: Unlike Euler angles, quaternions handle all attitudes seamlessly. Consequently, they prevent control system failures.

Interpolation and Smoothing: Spherical linear interpolation (SLERP) between quaternions creates smooth transitions. Thus, it suits trajectory planning well.

Integration with Filters: In multiplicative extended Kalman filters (MEKF), quaternions support error-state representations. They maintain unit norm and enhance stability in noisy environments.