A star tracker is an optical attitude sensor. It captures images of the starry sky and compares them with an internal star catalog (a database of star positions) to determine the spacecraft’s threeaxis attitude. The star tracker algorithm analyzes the positions of stars in the sky and calculates the vehicle’s orientation (attitude).
The complete star tracking algorithm usually consists of three critical stages. Each stage significantly affects the final accuracy and realtime performance.
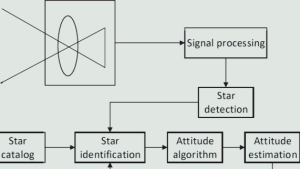
Star Centroid Extraction (Centroiding) — Achieving Subpixel Accuracy
This is the very first step of the entire algorithm.
Stars usually appear as slightly defocused, diffuse spots on the camera sensor (intentionally designed this way).
The algorithm must precisely extract the center position of each star spot.
Common methods include:
Threshold segmentation + connected component labeling — groups pixels brighter than a threshold into star spots.
Centroid calculation — the most classical and widely used method.
This is the most challenging part of the star tracker algorithm.
Especially in LostinSpace mode (no prior attitude information), the system must autonomously match the observed star pattern with the star catalog.
Mainstream algorithms can be classified as follows:
Triangle Algorithm — classic method proposed by Liebe. It forms triangles using three stars, calculates the three side lengths (angular distances), and searches for matches in the catalog.
Spherical Triangle Algorithm — accounts for celestial sphere curvature, suitable for widefieldofview systems.
Quad Method — faster hashtablebased approach (e.g. the method used by Astrometry.net).
Geometric Voting — star pairs vote based on angular distance; the pattern with the highest accumulated score wins.
Tetra Algorithm — modern hashtablebased method with nearoptimal time complexity, especially suitable for realtime applications.
Attitude Determination
After successfully identifying the stars, the algorithm matches the observed vectors (directions from the camera to the observed stars) with the reference vectors (celestial coordinates from the star catalog) and solves for the optimal rotation.
Classical and widely used methods include:
TRIAD algorithm — uses two pairs of vectors to construct an orthogonal triad. It is simple and fast but sensitive to noise.
QUEST algorithm (Quaternion Estimator) — proposed by Shuster. It solves the Wahba problem optimally using quaternions. It offers high accuracy with moderate computation — currently one of the most commonly used methods.
SVD algorithm (Singular Value Decomposition) — decomposes the attitude profile matrix. It is extremely robust.
Least Squares method — suitable for overdetermined systems (more than 2 stars), further reduces error.
High dynamic environments — rapid spacecraft maneuvers cause star trails and make prediction difficult.
Strong stray light — sunlight, moonlight, and Earth albedo enter the field of view.
Limited computing resources — very strict power and computation constraints on micro/nanosatellites.
Atmospheric interference — nearEarth platforms (airborne/missile) must operate 24/7.
Practical Applications of Star Trackers
Precise pointing for satellite constellations
Stable imaging for space telescopes
Autonomous navigation for deepspace probes
Allday navigation for airborne and missile platforms
Attitude determination for micro/nanosatellites and emerging commercial space projects
Send us a message,we will answer your email shortly!
TY-Space Technology (Beijing) Ltd. is professional focusing on advanced attitude optical sensors, especially Star Trackers for space industry.