
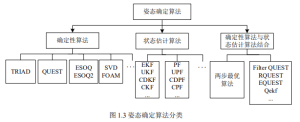
The attitude sensor (such as a star sensor) can measure observations related to the satellite’s attitude, and the problem of how to use these observations to obtain the satellite’s attitude is the problem of attitude determination. Attitude determination algorithms are divided into three categories: deterministic algorithms, state estimation algorithms, and a combination of the two.
The deterministic algorithm is a method of solving the current satellite attitude using the current measurement values, which is independent of the previous measurement values. The calculation principle is as follows:
![]()
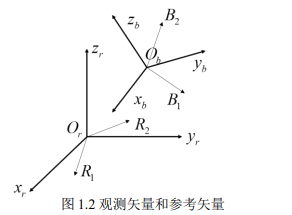
As shown in Figure 1.2. We can obtain the attitude of the satellite by solving A in the above formula, which is the transformation matrix between two coordinate systems.
Figure 1.2 Observation Vector and Reference Vector
Here are several classic and commonly used pose determination algorithms:
The TRIAD (ThRee-axis Attitude Determination) method is an algebraic method that is the earliest and simplest attitude determination algorithm. The basic principle is to use an attitude sensor to measure two observation vectors, and then use the measurement principle equation (1.1) above to obtain the satellite attitude. Shuster found in later research that the TRIAD method is feasible if there is no difference in accuracy between the second measurement vector and the first measurement vector; But if the accuracy is inconsistent, the condition of optimal orthogonal matrix cannot be met. In response to the issue of inconsistent accuracy between the two observation vectors mentioned above, BarItzhack proposed in 1997 that the optimal orthogonal matrix can be obtained by weighting and then repeating TRIAD twice.
In 1968, Davenport proposed the q method, which introduced the four elements of attitude to describe the attitude, greatly simplifying the optimal attitude solution in the sense of least squares. The HERO task was the earliest practical engineering application of the q method. The biggest drawback of this method is that the online calculation speed is very slow. Therefore, faster algorithms such as QUEST (Quaternion ESTimator) method and ESOQ (Estimator of the Optimal Quaternion) method have been proposed one after another. So far, QUEST remains one of the most widely used attitude determination algorithms.
The SVD (Singular Value Decomposition) method is another commonly used attitude determination algorithm proposed by Markley. The SVD method utilizes singular value decomposition for attitude determination, which has strong robustness. However, due to the high computational complexity of singular value decomposition, its calculation speed is relatively slow. To this end, Markley made improvements to the SVD algorithm and proposed the FOAM (Fast Optical Attention Matrix) method.
In 2000, Markley and Mortari comprehensively compared these attitude determination algorithms based on the q method from various perspectives such as accuracy, complexity, and speed, and believed that the QUEST method and ESOQ2 method were the best compared methods.
In recent years, although there have been no new deterministic algorithms, with the continuous exploration of the essence of the Wahba problem, people have gained a deeper understanding of deterministic algorithms, mainly recognizing the relationship between existing deterministic algorithms and maximum likelihood estimation.
Summarizing the numerous deterministic algorithms mentioned above, it can be found that deterministic methods have the advantages of simplicity, clear principles, and the absence of the need for initial values. However, it requires high measurement reference vector accuracy, otherwise the error of deterministic algorithms will be significant. Moreover, deterministic algorithms still have many problems, such as the inability to eliminate the impact of measurement errors and the high computational complexity. In this case, attitude estimation algorithms have entered people’s field of vision.
In the state estimation algorithm, we can establish the state variable ourselves and estimate the uncertain parameter of gyro drift as a part of the state variable. The state estimation method establishes satellite attitude kinematics, dynamics equations, and measurement equations for selected sensors, and uses the state of the previous moment to estimate the state variables at that moment. In the late 1970s and early 1980s, Kalman Filter (KF) was used to filter and estimate noise measurements for attitude and gyro deviations, providing higher accuracy than deterministic methods. In order to solve the problem of high computational complexity and easy divergence in spacecraft attitude determination, a lot of work has been carried out to improve the Kalman filter. EKF is the core of real-time spacecraft attitude estimation, and most attitude determination EKF uses attitude parameters at lower latitudes than the nine parameter attitude matrix. Due to the singularity or discontinuity of the three parameter attitudes, this has led to the development of constraint attitude representation in EKF. EKF, especially Multiplicative Extended Kalman Filter (MEKF), performs well in the vast majority of attitude determination applications. Due to the inherent problems of EKF linearization process, weak robustness, and poor filtering performance for strongly nonlinear systems, some new filters have emerged. For example, unscented Kalman Filter (UKF) , Center Difference Kalman Filter (CDKF) , Cubature Kalman Filter (CKF), etc.
However, Kalman filters require prior knowledge of modeling errors or system noise, which may not be suitable for practical applications. More specifically, when using a Kalman filter, the system noise should conform to a white Gaussian distribution, whereas previously, satellites were unable to obtain the size and distribution of the noise. In this case, other filters such as Predictive Filter (PF) , Unscented Predictive Filter (UPF), Cubature Predictive Filter (CPF), Center Difference Predictive Filter (CDPF)]. Predictive Variable Structure Filter (PVSF) is proposed for attitude estimation. Meanwhile, particle filters and robust filters are also used for attitude estimation.
However, the use of filter based attitude estimation algorithms in practical applications is relatively limited and requires careful selection.
Deterministic algorithms and state estimation algorithms each have their own advantages and disadvantages, leading to the emergence of some methods that combine the two. These methods are divided into two categories. One method is a two-step optimal estimation: the first step is to convert the measurement equation into a linear equation to provide a linear filter design, and the second step is a least squares estimation. For example, the results of a vector sensor are first decomposed into a linear measurement equation through SVD, and then input into filters such as EKF and UKF. Another method is to use some attitude determination methods to derive simplified filters and reconstruct the basic structure of EKF. For example, simple filters based on QUEST include filter QUEST and recursive QUEST (RQUEST). There are also more complex and robust methods called Extended QUEST (EQUEST), which use a complete nonlinear propagation and a new measurement update. In addition, Thomas proposed a filter called qEKF that combines the q method with EKF. The performance of qEKF and EQUEST has been verified to be equivalent.
Figure 1.3 Classification of pose determination algorithms
A satellite attitude determination scheme using a combination of star sensors/gyroscopes for measurement. The principles of Kalman filtering algorithm and extended Kalman filtering algorithm were studied, and the model and algorithm flow of star sensor/gyroscope combined attitude determination system based on extended Kalman filtering were analyzed in detail. To address the issue of its divergence, this paper proposes a two-step optimal estimation algorithm based on the improved Q-method. The improved Q-method, which can output continuous quaternions, is used to first process the observation vector of the star sensor. The calculated quaternion is used as the measurement data of the Kalman filter, so that the measurement equation is a linear equation without linearization.
Send us a message,we will answer your email shortly!